問 2.5.2-1(第 2 章 p.12)
真偽値のリスト [Bool]を 2進数と見なして、対応する整数を計算
する関数 fromBin :: [Bool] -> Integer を定義せよ。例えば、
fromBin [True,True] は 3、 fromBin [True,False,True,False] は 10になる。
ヒント: 引数の数を一つ増やした補助関数が必要になる。
ヒント: ホーナーの方法を使う。例えば
fromBin [True,False,True,False] は
\((1 \times 2 + 0) \times 2 + 1) \times 2 + 0\)、
fromBin [True,True,False,True] は
\((1 \times 2 + 1) \times 2 + 0) \times 2 + 1\)
となるように計算する。
問 2.5.2-2 (第 2 章 p.12)
真偽値のリスト [Bool]を 2進数と見なして、対応する整数を計算
する関数 fromBinRev :: [Bool] -> Integer を定義せよ。
ただし、先の問とは逆順に真偽値がならんでいると仮定せよ。例えば、
fromBinRev [True,True,False,True] は
\( 1 + 2 \times (1 + 2 \times (0 + 2 \times 1)) = 11_{(10)}\)
となる。
問 2.6.1 (第 2 章 p.14)
すべての有限リスト xs について、
- xs ++ [] = xs
- (xs ++ ys) ++ zs = xs ++ (ys ++ zs)
が成り立つことを xs に関する帰納法で証明せよ。 (どこで帰納法の仮定を使用するか明示せよ。 さらに (++) の定義の等式:
[] ++ ys = ys -- ① (x:xs) ++ ys = x : (xs ++ ys) -- ②を使った場合は、①, ② をラベル付けせよ。 帰納法の仮定を使った場合は、⑨ をラベル付けせよ。 )
ただし (++) は、 プリント第 2 章 p.13 で定義が示されている関数である。
問 2.11.3 (第 2 章 p.22)
要素に重複のない昇順に並んだ2つのリストをマージして、やはり重複なし
の昇順のリストを生成する関数 merge を定義せよ。
問 2.12.3 (第 2 章 p.23)
非負の整数 \(n\) を受け取り、
\(1 \le x \lt y \lt z \le n\)
の範囲で
\(x^2 + y^2 = z^2\)
となるすべての x, y, z
の組を生成する関数
chokkaku :: Integer -> [(Integer,Integer,Integer)]を内包表記を用いて定義せよ。
(挑戦・非必須)(ナイト巡回)問 2.13.4 (第 2 章 p.28)
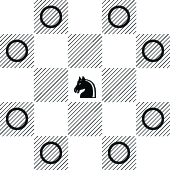
ナイトは、右の図の中央のマスから○印のマスへ
移動できるチェスのコマである。5 × 5マスのチェス盤で、あるマス
(例えば、左上隅)から始めてすべてのマスを 1 回ずつ訪れる経路を求めるプログラムを作成せよ。
Tree 型に対して、次のような関数を定義せよ。
preorder :: Tree a -> [a] -- 前順走査
inorder :: Tree a -> [a] -- 中順走査
postorder :: Tree a -> [a] -- 後順走査
例えば、
② preorder tree4, ③ inorder tree4,
④ postorder tree4 の結果はそれぞれ、
② [2,1,3,4], ③ [1,2,3,4],
④ [1,4,3,2]
となる。
組込みのリスト型と等価なデータ型
data MyList a = MyNil | MyCons a (MyList a)
を、deriving を用いずに、Eq クラスと Ord クラスのインスタンスとして宣言せよ。 Ord クラスのメソッドにはいわゆる 辞書式の順序を用いよ。
(クラスの定義中にデフォルトの実装が定義されているので、Eq クラ スの == メソッドと Ord クラスの <= メソッドだけを 定義すれば、他のメソッドの定義は自動的に生成される。)
ヒント: 次のような、リストから MyList への変換を行う 関数を定義して、
toMyList :: [a] -> MyList a toMyList [] = MyNil toMyList (x:xs) = MyCons x (toMyList xs)
いくつかのケースをテストせよ。
toMyList "abc" <= toMyList "abd" -- True toMyList "ab" <= toMyList "abc" -- True toMyList "ab" <= toMyList "a" -- False toMyList "ab" <= toMyList "ba" -- True