問 2.5.2-1(第 2 章 p.12)
真偽値のリスト [Bool]を 2進数と見なして、対応する整数を計算
する関数 fromBin :: [Bool] -> Integer を定義せよ。例えば、
fromBin [True,True] は 3、 fromBin [True,False,True,False] は 10になる。
ヒント: 引数の数を一つ増やした補助関数が必要になる。
ヒント: ホーナーの方法を使う。例えば
fromBin [True,False,True,False] は
\((1 \times 2 + 0) \times 2 + 1) \times 2 + 0\)、
fromBin [True,True,False,True] は
\((1 \times 2 + 1) \times 2 + 0) \times 2 + 1\)
となるように計算する。
問 2.5.2-2 (第 2 章 p.12)
真偽値のリスト [Bool]を 2進数と見なして、対応する整数を計算
する関数 fromBinRev :: [Bool] -> Integer を定義せよ。
ただし、先の問とは逆順に真偽値がならんでいると仮定せよ。例えば、
fromBinRev [True,True,False,True] は
\( 1 + 2 \times (1 + 2 \times (0 + 2 \times 1)) = 11_{(10)}\)
となる。
問 2.5.4 (第 2 章 p.12)
2つの引数 x, xsを受け取り、リスト xs から
xと等しい要素を
- もっとも先頭に現れる一つの要素だけ取り除いたリストを返す関数
deleteOne - すべて取り除いたリストを返す関数
deleteAll
をそれぞれ定義せよ。
問 2.6.2 (第 2 章 p.14)
すべての有限リスト xs について、
- xs ++ [] = xs
- (xs ++ ys) ++ zs = xs ++ (ys ++ zs)
が成り立つことを xs に関する帰納法で証明せよ。 (どこで帰納法の仮定を使用するか明示せよ。 さらに (++) の定義の等式:
[] ++ ys = ys -- ① (x:xs) ++ ys = x : (xs ++ ys) -- ②を使った場合は、①, ② をラベル付けせよ。 帰納法の仮定を使った場合は、⑨ をラベル付けせよ。 )
ただし (++) は、 プリント第 2 章 p.13 で定義が示されている関数である。
問 2.7.1 (第 2 章 p.16)
これらの関数(や以前に紹介した関数)を使って、次のような関数を定義せよ。
- 2つのリストの 0番目の要素同士、1番目の要素同士、… を比較し、
等しい要素の個数を返す関数
countEq例えばcountEq [1,2,3,5] [2,2,6,5,3]は 2になる。 -
文字列のリストを受け取り、各文字列の最後に “
;” をつけて 連接した文字列を返すaddSemicolon例えばaddSemicolon ["abc","xyz","123"]は"abc;xyz;123;"になる。
問 2.12.2 (第 2 章 p.23)
非負の整数 \(n\) を受け取り、\( 0 \le x \le y \le n\) となるすべての \(x, y\)
の組を生成する関数 foo :: Integer -> [(Integer, Integer)]
を内包表記を用いて定義せよ。
ヒント: .. を使う。
問 2.12.3 (第 2 章 p.23)
非負の整数 \(n\) を受け取り、
\(1 \le x \lt y \lt z \le n\)
の範囲で
\(x^2 + y^2 = z^2\)
となるすべての \(x, y, z\)
の組を生成する関数
chokkaku :: Integer -> [(Integer,Integer,Integer)]を内包表記を用いて定義せよ。
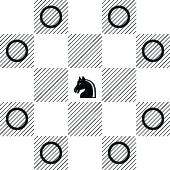
(挑戦・非必須)(ナイト巡回)問 2.13.4 (第 2 章 p.28)
ナイトは、右の図の中央のマスから○印のマスへ
移動できるチェスのコマである。5 × 5マスのチェス盤で、あるマス
(例えば、左上隅)から始めてすべてのマスを 1 回ずつ訪れる経路を求めるプログラムを作成せよ。
Tree 型に対して、次のような関数を定義せよ。
preorder :: Tree a -> [a] -- 前順走査
inorder :: Tree a -> [a] -- 中順走査
postorder :: Tree a -> [a] -- 後順走査
例えば、
② preorder tree4, ③ inorder tree4,
④ postorder tree4 の結果はそれぞれ、
② [2,1,3,4], ③ [1,2,3,4],
④ [1,4,3,2]
となる。
組込みのリスト型と等価なデータ型
data MyList a = MyNil | MyCons a (MyList a)
を、deriving を用いずに、Eq クラスと Ord クラスのインスタンスとして宣言せよ。 Ord クラスのメソッドにはいわゆる 辞書式の順序を用いよ。
(クラスの定義中にデフォルトの実装が定義されているので、Eq クラ スの == メソッドと Ord クラスの <= メソッドだけを 定義すれば、他のメソッドの定義は自動的に生成される。)
ヒント: 次のような、リストから MyList への変換を行う 関数を定義して、
toMyList :: [a] -> MyList a toMyList [] = MyNil toMyList (x:xs) = MyCons x (toMyList xs)
いくつかのケースをテストせよ。
toMyList "abc" <= toMyList "abd" -- True toMyList "ab" <= toMyList "abc" -- True toMyList "ab" <= toMyList "a" -- False toMyList "ab" <= toMyList "ba" -- True